Dealing with imbalanced data: undersampling, oversampling and proper cross-validation

[For this analysis I used the term/preterm dataset that you can find on Physionet. My data and code are also available on github]

A couple of weeks ago I read this post about cross-validation done wrong. During cross-validation, we are typically trying to understand how well our model can generalize, and how well it can predict our outcome of interest on unseen samples. The author of the blog post makes some good points, especially about feature selection. It is indeed common malpractice to perform feature selection before we go into cross-validation, something that should however be done during cross-validation, so that the selected features are only derived from training data, and not from pooled training and validation data.

However, the article doesn’t touch a problem that is a major issue in most clinical research, i.e. how to properly cross-validate when we have imbalanced data. As a matter of fact, in the context of many medical applications, we have datasets where we have two classes for the main outcome; normal samples and relevant samples. For example in a cancer detection application we might have a small percentages of patients with cancer (relevant samples) while the majority of samples might be healthy individuals. Outside of the medical space, this is true (even more) for the case for example of fraud detection, where the rate of relevant samples (i.e. frauds) to normal samples might be even in the order of 1 to 100 000.

problem at hand

The main motivation behind the need to preprocess imbalanced data before we feed them into a classifier is that typically classifiers are more sensitive to detecting the majority class and less sensitive to the minority class. Thus, if we don't take care of the issue, the classification output will be biased, in many cases resulting in always predicting the majority class. Many methods have been proposed in the past few years to deal with imbalanced data. This is not really my area of research, however since I started working on preterm birth prediction, I had to deal with the problem more often. Preterm birth refers to pregnancies shorter than 37 weeks, and results in about 6-7% of all deliveries in most European countries, and 11% of all deliveries in the U.S., therefore the data are quite imbalanced.

I recently came across two papers [1, 2] predicting term and preterm deliveries using Electrohysterography (EHG) data. The authors used one single cross-sectional EHG recording (capturing the electrical activity of the uterus) and claimed near perfect accuracy in discriminating between the two classes (AUC value of 0.99 [2], compared to AUC = 0.52-0.60 without oversampling).

This seemed to me like a clear case of overfitting and bad cross-validation, for a couple of reasons. First of all, let’s just look at the data:

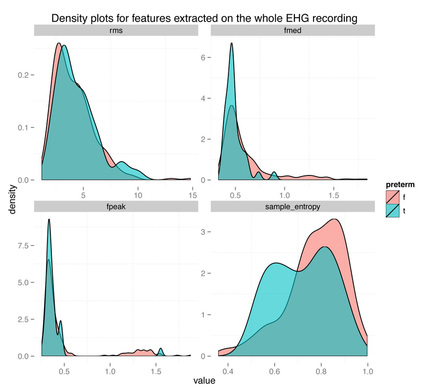
The density plots above show the feature's distribution for four features over the two classes, term and preterm (f = false, the delivery was not preterm, in light red, t = true, the delivery was preterm, in light blue). As we can see there is really not much discriminative power here between conditions. The extracted features are completely overlapping between the two classes and we might have a "garbage in, garbage out" issue, more than a "this is not enough data" issue. 

Just thinking about the problem domain, should also raise some doubts, when we see results as high as auc = 0.99. The term/preterm distinction is almost arbitrary, set to 37 weeks of pregnancy. If you deliver at 36 weeks and 6 days, you are labeled preterm. On the other hand, if you deliver at 37 weeks and 1 day, you are labeled term. Obviously, there is no actual difference due to being term or preterm between two people that deliver that close, it's just a convention, and as such, prediction results will always be affected and most likely very inaccurate around the 37 weeks threshold.

Since the dataset used is available for anyone to download and use from Physionet, in this post I will partially replicate the published results, and show how to properly cross-validate when oversampling data. Maybe some clarification on this issue will help in avoiding the same mistakes in the future.

dataset, features, performance measures and cross-validation technique

Dataset
A few notes on what I will be using. The dataset was collected in Slovenia at the University Medical Centre Ljubljana, Department of Obstetrics and Gynecology, between 1997 and 2005. It consists of cross-sectional EHG data for non-at-risk singleton pregnancies. The dataset is imbalanced with 38 out of 300 recordings that are preterm. More information about the dataset can be found in [3]. To keep things simple, the main rationale behind this data is that EHG measures the electrical activity of the uterus, that clearly changes during pregnancy, until it results in contractions, labour and delivery. Therefore, the researchers speculated that by monitoring the activity of the uterus non-invasively early on, it could be possible to determine which pregnancies will result in preterm deliveries. 

Features and classifiers
On Physionet, you can find even the raw data for this study, however to keep things even simpler, for this analysis I will be using another file the authors provided, where data has already been filtered in the relevant frequency for EHG activity, and features have already been extracted. We have four features (root mean square of the EHG signal, median frequency, frequency peak and sample entropy, again have a look at the paper here for more information on how these features are computed). According to the researchers that collected the dataset, the most informative channel is channel 3, probably due to it's position, and therefore I will be using precomputed features extracted from channel 3. The exact data is also on github. As classifiers, I used a bunch of common classifiers, logistic regression, classification trees, SVMs and random forests. I won't do any feature selection, but use all the four features we have.

Performance metrics
As performance metrics I will use sensitivity, specificity and AUC. See wikipedia for a clear description of these metrics.

Cross-validation technique
I decided to cross-validate using leave one participant out cross-validation. This technique leaves no room for mistakes when using the dataset as it is or when undersampling. However, when oversampling, things are very different. So let's move on to the analysis.

imbalanced data

What can we do when we have imbalanced data? Mainly three things:

• Ignoring the problem.
  
• Undersampling the majority class.
  
• Oversampling the minority class.
  

ignoring the problem

Building a classifier using the data as it is, would in most cases give us a prediction model that always returns the majority class. The classifier would be biased. Let's build the models:

From the code above we can see that at each iteration I simply select the current index as the validation one, and build the model using the remaining data (i.e. the training data). Results:

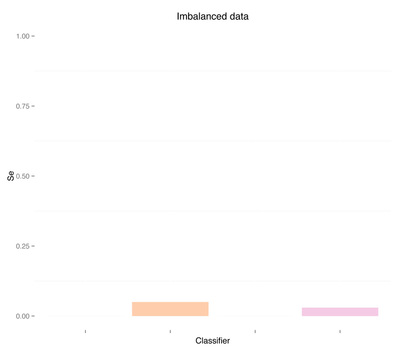
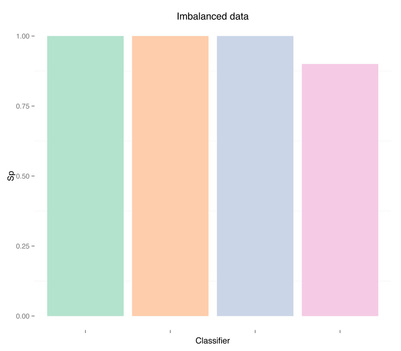
As expected the classifier is biased, and sensitivity is zero or very close to zero, while specificity is one or very close to one, i.e. all or almost all recordings are detected as term, and therefore no or almost no preterm recordings are correctly identified. Let's move on to the next case, undersampling the majority class.

undersampling the majority class

One of the most common and simplest strategies to handle imbalanced data is to undersample the majority class. While different techniques have been proposed in the past, typically using more advanced methods (e.g. undersampling specific samples, for examples the ones “further away from the decision boundary” [4]) did not bring any improvement with respect to simply selecting samples at random. So, for this analysis I will simply select n samples at random from the majority class, where n is the number of samples for the minority class, and use them during training phase, after excluding the sample to use for validation. Here is the code:

As mentioned above, the main difference from the previous script is that now we randomly select at each iteration n samples from the majority class, and use only those as training data, combined with all samples from the minority class. Let's look at the results:

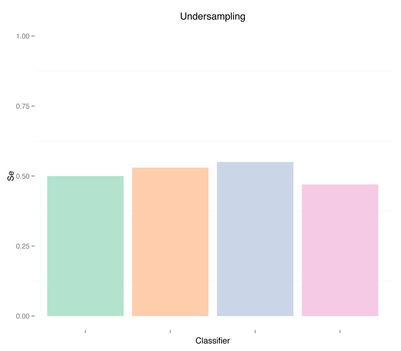
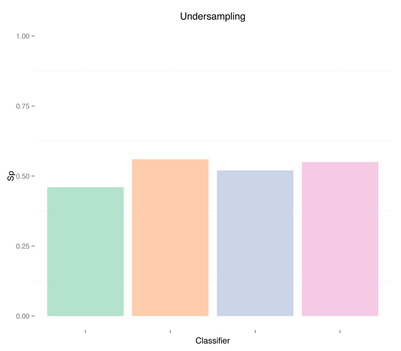
By undersampling, we solved the class imbalance issue, and increased the sensitivity of our models. However, results are very poor. A reason could indeed be that we trained our classifiers using few samples. In general, the more imbalanced the dataset the more samples will be discarded when undersampling, therefore throwing away potentially useful information. The question we should ask ourselves now is, are we developing a poor classifier because we don’t have much data? Or are we simply relying on bad features with poor discriminative power, and therefore more data of the same type won’t necessary help? 

oversampling the minority class

Oversampling the minority class can result in overfitting problems if we oversample before cross-validating. What is wrong with oversampling before cross-validating? Let’s consider the simplest oversampling method ever, as an example that clearly explains this point.

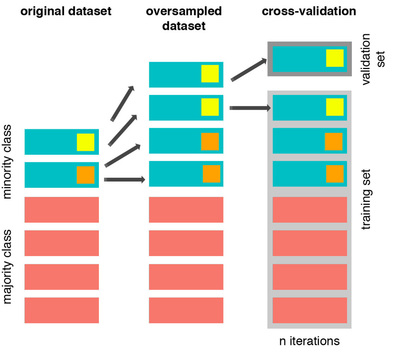
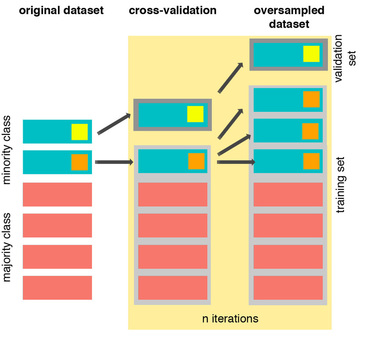
The easiest way to oversample is to re-sample the minority class, i.e. to duplicate the entries, or manufacture data which is exactly the same as what we have already. Now, if we do so before cross-validating, i.e. before we enter the leave one participant out cross-validation loop, we will be training the classifier using N-1 entries, leaving 1 out, but including in the N-1 one or more instances that are exactly the same as the one being validated. Thus, defeating the purpose of cross-validation altogether. Let's have a look at this issue graphically:

From left to right, we start with the original dataset where we have a minority class with two samples. We duplicate those samples, and then we do cross-validation. At this point there will be iterations, such as the one showed, where the training and validation set contain the same sample, resulting in overfitting and misleading results. Here is how this should be done:

First, we start cross-validating. This means that at each iteration we first exclude the sample to use as validation set, and then oversample the remaining of the minority class (in orange). In this toy example I had only two samples, so I created three instances of the same. The difference from before, is that clearly now we are not using the same data for training and validation. Therefore we will obtain more representative results. The same holds even if we use other cross-validation methods, such as k-fold cross-validation.

This was a simple example, and better methods can be used to oversample. One of the most common being the SMOTE technique, i.e. a method that instead of simply duplicating entries creates entries that are interpolations of the minority class, as well as undersamples the majority class. Normally when we duplicate data points the classifiers get very convinced about a specific data point with small boundaries around it, as the only point where the minority class is valid, instead of generalizing from it. However, SMOTE effectively forces the decision region of the minority class to become more general, partially solving the generalization problem. There are some pretty neat visualizations in the original paper, so I would advice to have a look here. 

However, something to keep in mind is that while oversampling using SMOTE does improve the decision boundaries, it has nothing to do with cross-validation. If we use the same data for training and validation, results will be dramatically better than what they would be with out of sample data. The same problem that I highlighted above with a simpler example, is still present. Let’s see what results we can get when oversampling before cross-validation.

Bad cross-validation when oversampling
Here is the code, we first oversample then we go into the cross-validation loop, with our synthetic samples that are basically interpolations of the original ones:

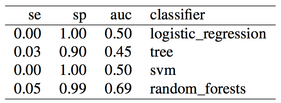
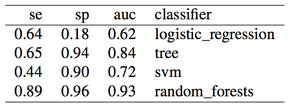
The SMOTE function is part of the DMwR R package. Here are the results:

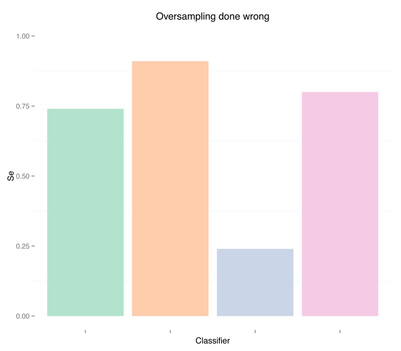
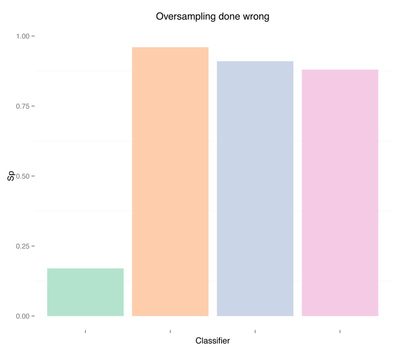
Results are pretty good now. Especially for random forests, we obtained auc = 0.93 without any feature engineering, simply using what was provided in the dataset, and without any parameter tuning for the classifier. Once again, apart from the differences in the two oversampling methods (replication of the minority class or SMOTE), the issue here is not even which method to use, but when to use it. Using oversampling before cross-validation we have now obtained almost perfect accuracy, i.e. we overfitted (even a simple classification tree gets auc = 0.84). 

Proper cross-validation when oversampling
The way to proper cross validate when oversampling data is rather simple. Exactly like we should do feature selection inside the cross validation loop, we should also oversample inside the loop. It makes no sense to create instances based on our current minority class and then exclude an instance for validation, pretending we didn’t generate it using data that is still in the training set. This time we oversample inside the cross-validation loop, after the validation sample has already been removed from the training data, so that we create synthetic data by interpolating only recordings that will not be used for validation. Our cross validation iterations will now be the same as the number of your samples. See the code:

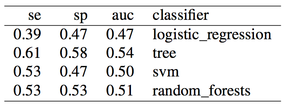
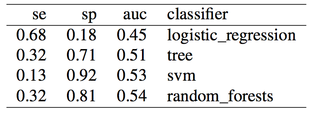
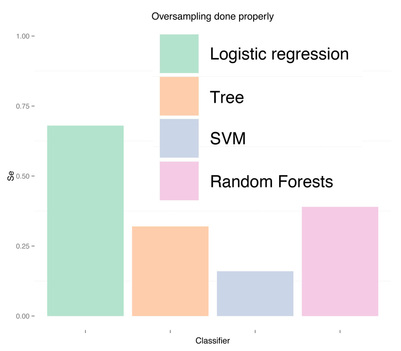
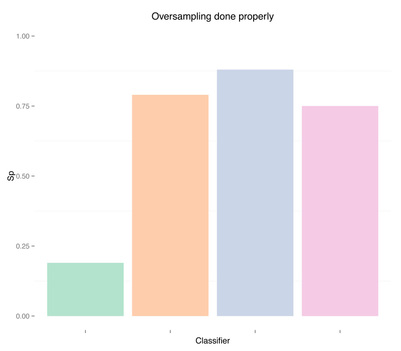
And finally, results when doing proper cross-validation with oversampling using the SMOTE technique:

As expected, more data didn't solve any problem, regardless of doing "smart" oversampling using SMOTE. What did bring very high accuracy, was simply overfitting. Here are a few final plots summarizing sensitivity and specificity results from the analysis performed in this post.

Sensitivity

Specificity

As we can see oversampling properly (fourth plots) is not much better than undersampling (second plots), for this dataset.

summary

In this post I used imbalanced EHG recordings to predict term and preterm deliveries, with the main goal of understanding how to properly cross-validate when oversampling is used. Hopefully, it is now clear that oversampling must be part of the cross-validation and not done before. 

To summarize, when cross-validating with oversampling, do the following to make sure your results are generalizable:

• Inside the cross-validation loop, get a sample out and do not use it for anything related to features selection, oversampling or model building.
  
• Oversample your minority class, without the sample you already excluded.
  
• Use the excluded sample for validation, and the oversampled minority class + the majority class, to create the model.
  
• Repeat n times, where n is your number of samples (if doing leave one participant out cross-validation).

A note on EHG data, pregnancy, delivery and term/preterm classification

Obviously, this analysis does not mean that detecting term and preterm recordings with EHG data is not possible. It simply means that one single cross-sectional recording and these basic features do not seem to be sufficient. Most likely what is needed here are longitudinal recordings of multiple physiological signals (e.g. EHG, ECG, fetal ECG, HR/HRV, etc.) as well as information about activity and behavior. Multi-parameter longitudinal data can help better understanding variations in such signals with respect to pregnancy outcomes as well as modeling individual differences, similarly to what we see in other complex applications which are poorly understood from a physiological point of view. At Bloom we're working at better modeling these variables to effectively predict preterm birth risk. However, intrinsic limitations to this problem are present, simply because of how the reference is defined (i.e. an almost arbitrary threshold at 37 weeks), and therefore claims of near-perfect classification should be analyzed with care, as we've seen in this post. 

references

[1] Fergus, Paul, et al. "Prediction of preterm deliveries from EHG signals using machine learning." (2013): e77154. PloS one.
[2] Ren, Peng, et al. "Improved Prediction of Preterm Delivery Using Empirical Mode Decomposition Analysis of Uterine Electromyography Signals." PloS one. 10.7 (2015): e0132116.
[3] Fele-Žorž, Gašper, et al. "A comparison of various linear and non-linear signal processing techniques to separate uterine EMG records of term and pre-term delivery groups." Medical & biological engineering & computing 46.9 (2008): 911-922.
[4] Japkowicz, N. (2000). The Class Imbalance Problem: Significance and Strategies. In Proceedings of the 200 International Conference on Artificial Intelligence (IC-AI’2000): Special Track on Inductive Learning Las Vegas, Nevada.
[5] Chawla, Nitesh V., et al. "SMOTE: synthetic minority over-sampling technique."Journal of artificial intelligence research (2002): 321-357.

Follow @marco_alt